Why are Visuo-spatial Representations Sometimes Weird?
Rodrigo Garro Rivero, USC
In cognitive science and philosophy, researchers hypothesize about the formats of mental representations via analogies to artifactual representations such as sentences, maps, pictures, etc. The guiding assumption is that if our mental representations were to be structured as artifactual representations, then they would exhibit characteristic patterns of performance that reflect the structural features of the artifactual representation [let’s call this the Artifactual Assumption]. Even though the Artifactual Assumption has proven productive in cognitive science and philosophy, I worry that it sometimes leads us down the wrong path.
In this post, I illustrate this with a case study. Recently, it has been argued that humans use a system of mental Polar coordinates to represent small-scale visuo-spatial relations (Yang and Flombaum, 2018; Yousif and Keil, 2021; Yousif, 2022). Particularly, researchers have found evidence that visuospatial relations are often represented by independent pairings of angle and distance, which compose much like the polar coordinates we might discuss in the math class. Given the Artefactual Assumption, it might then seem natural to expect the structure of familiar polar coordinates to match these mental representations in other respects — e.g., as composing from digital (symbolic) constituents. However, on inspection, I suggest that we find crucial differences. To fully explain the empirical data, I think we need to understand the relevant mental representations comprising analog instead of digital constituents.
Experiment
I focus on a case study by Yousif and Keil (2021) who hypothesized that if observers use polar coordinates to represent space, they will represent angle and distance independently. To test the hypothesis, researchers conducted visual matching task experiments (see Figure 1). In these experiments, observers were presented with a set of shapes at the top of the display and one or no shapes at the bottom. Their task was to drag the missing shape(s) with the mouse and locate them relative to the others, matching the relative positions of the shapes at the top of the display. Since this task was hard to do perfectly, the researchers then analyzed the patterns of errors that observers had made in placing the missing shape(s).
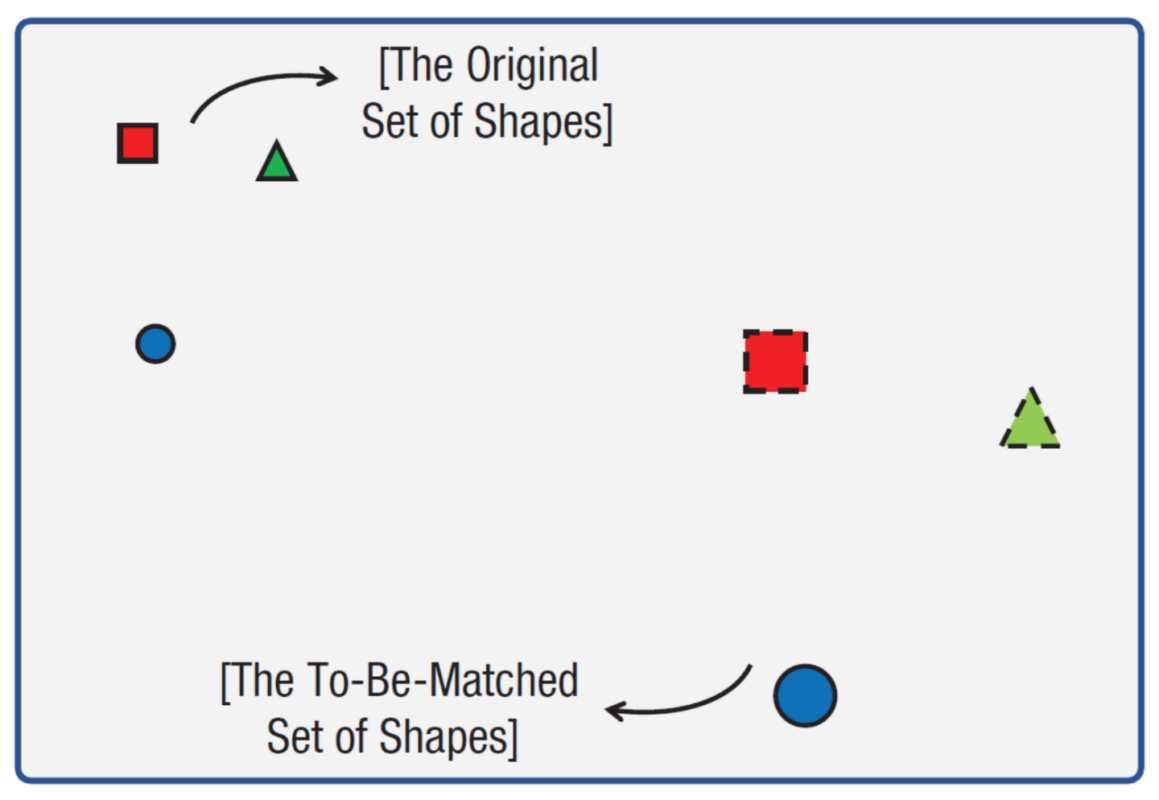
Figure 1
The data revealed at least two patterns of errors in participants’ performance. First, participants’ errors in representing angle and distance were independent of each other. I call this Independent-error. Second, participants’ errors in placing the missing shape were nevertheless centered around the target location along both angle and distance dimensions. I call this Centered-error. The first error has served as crucial evidence that visuospatial representations are encoded in a polar coordinate format. Since polar coordinates consist of an independent pairing of angle and distance symbols, the errors in angle and distance should also be independent (Yousif and Keil, 2021; see Yousif, 2022 for alternative hypotheses). However, Centered errors have been overlooked, most likely since they seem consistent with the structural features of polar coordinates. In what follows, I offer an abductive argument that Centered-errors are best explained by understanding the constituents of these mental Polar coordinates as analog rather than digital.
Analog coordinates
Let me introduce the distinction between analog and digital. Unlike traditional views, I prefer the notion of analog representations, which hold that they have a mirroring feature. That is, the vehicles of analog representations mirror what they represent (Maley, 2011; Beck, 2018; Clarke, 2021). Think of a mercury thermometer, where the higher the mercury height (the vehicle of representation), the higher the temperature (what is represented). The mercury level varies as a monotonic function of the temperature represented, thereby serving as an analog of its content. In contrast, digital representations stand in an arbitrary relationship with what is represented. In the case of a digital thermometer, the digits — i.e., the Arabic numerals — stand in an arbitrary relationship to the temperature.
How does this relate to the Centered-errors, described above?
First, suppose that the constituents of the polar coordinates are analog — i.e., angle and distance representation are represented by analog representations, whose content-bearing vehicle properties mirror, or bear some kind of isomorphism to the angle and distance values being represented. This offers a rough and ready explanation for the Centered-errors that we wish to explain.
To illustrate, consider an analog system that I’ll call Ana. Ana’s task is to count the number of goals in a soccer match. She pours a cupful of water, containing 200ml, into a bucket every time one team scores a goal. If the team scores 4 goals, then the bucket contains 800ml. Here, the volume of water (the vehicle of representation) mirrors the number of goals (what is represented), thus representing the number of goals in an analog format.
Of course, in reality, Ana is noisy. And this means that, in some cases, we will often confuse similar numbers of goals. For instance, suppose that each cup fails to contain exactly 200ml of water, but instead contains somewhere between 180 and 220ml, and that we find ourselves in a situation where Ana’s bucket contains 1980 ml. Here, the number of goals that have been counted is underdetermined by the water volume. It could be that the team has scored 9 goals (1620 ml – 1980 ml), 10 goals (1800 ml – 2200 ml), or 11 goals (1980 ml – 2420 ml). 1980ml is within all these ranges. But while we might sometimes confuse nearby values in precisely this way, it would be very odd to confuse values far from the actual value. For instance, it’s unlikely that Ana pours 9000ml of water into her bucket when the team has scored only 10 goals.
Having considered the toy model, let’s apply it to the polar coordinate constituents. We can conceptualize that a physical magnitude in the brain mirrors the distance of an object. Suppose that 1cm is represented by the symbol “_”, 2 cm is represented by “__”, 3 cm is represented by “___”, 4cm is represented by “____”, and so on (Carey, 2009). This offers to explain Centered-errors. Just as Ana confuses similar numbers of goals, our visual system can now be expected to confuse similar distances, given noise of an analogous sort. This is because the vehicle that represents 5cm is literally more similar to the vehicle that represents 4.5cm than to the vehicle that represents 4cm.
By contrast, suppose that angle and distance symbols that our mental polar coordinate system comprises have a digital structure. Consider a digital system, DJ, representing sprint times using digital symbols. Here, 10 seconds might be represented by ‘10’, ‘1010’, ‘A’, ‘X’, etc., but for the sake of simplicity, let’s assume that it uses Arabic numerals. If a runner takes 33s to complete the race, then DJ writes on a paper the symbol “33”.
So far, so good. The trouble is, it’s hard to see how this can be used to explain centered errors. This is not because DJ is immune to noise in the production of its symbols. After all, it might run out of ink and write ‘30.3’ instead of 30.3, or have a messy handwriting, writing ‘7’ instead of ‘1’. The trouble is that, here, such noise fails to imply any kind of Centered error. Prima facie, 30.3 is more likely to be confused with 303 than 29, and ‘7’ is more likely to be confused with 1 than 8. Indeed, this seems to be a straightforward implication of the use of digital symbols, whose content bearing properties sit arbitrarily related to their contents. Thus, it is less clear how a system of digital representations in the head should explain Centered-error.
Conclusion
Summing up, a polar coordinate structure explains the Independent-errors. Yet, if we were to meekly follow the Artefactual Assumption, we would expect the constituents of the polar coordinates to be digital. In contrast, by considering the constituents as analog, we have a straightforward explanation of Centered-errors. As a result, we have an interesting hybrid representation: a polar coordinate comprising analog constituents.
References:
Beck, Jacob (2018). Analog Mental Representation. WIREs Cognitive Science.
Carey, Susan (2009). The origin of concepts. New York: Oxford University Press.Clarke, Sam
Clarke, Sam (2021). Mapping the Visual Icon. Philosophical Quarterly 72 (3):552-577.
Clarke, Sam (2023). Compositionality and constituent structure in the analogue mind. Philosophical Perspectives 37 (1):90-118.
Dehaene, S. (1997) The Number Sense: How the Mind Creates Mathematics. Oxford: OUP.
Maley, Corey J. (2011). Analog and digital, continuous and discrete. Philosophical Studies 155 (1):117-131.
Yang, Feitong & Flombaum, Jonathan (2018). Polar coordinates as the format of spatial representation in visual perception. Journal of Vision, 18(10):21.
Yousif, S. R., Chen, Y. C., & Scholl, B. J. (2020). Systematic angular biases in the representation of visual space. Attention, Perception, & Psychophysics, 82, 3124–3143.
Yousif, S. R., & Keil, F. C. (2021). The shape of space: Evidence for spontaneous but flexible use of polar coordinates in visuospatial representations. Psychological Science, 32, 573–586
Yousif, S. R. (2022). Redundancy and Reducibility in the Formats of Spatial Representations. Perspectives on Psychological Science, 17(6), 1778-1793.

